二分查找

二分查找的思想

二分查找（Binary Search）算法，也叫折半查找算法。

二分查找针对的是一个有序的数据集合，查找思想有点类似分治思想。每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为 0。

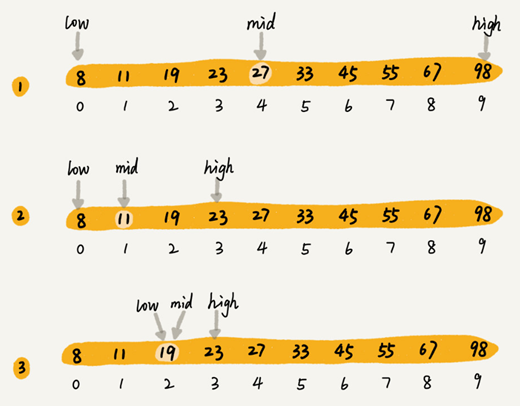
假设有 1000 条订单数据，已经按照订单金额从小到大排序，每个订单金额都不同，并且最小单位是元。现在想知道是否存在金额等于 19 元的订单。如果存在，则返回订单数据，如果不存在则返回 null。

利用二分思想，每次都与区间的中间数据比对大小，缩小查找区间的范围。下图中，low 和 high 表示待查找区间的下标，mid 表示待查找区间的中间元素下标。

1570440501975

二分查找的时间复杂度为O(logn) ，被查找区间的大小变化：

$$ n, \frac{n}{2}, \frac{n}{4}, \frac{n}{8}, \cdots, \frac{n}{2^{k}} \cdots $$

二分查找的实现

最简单的情况就是有序数组中不存在重复元素， Java 代码循环实现：

public int bsearch(int[] a, int n, int value) {  int low = 0;  int high = n - 1;  while (low <= high) {    int mid = (low + high) / 2;    if (a[mid] == value) {      return mid;    } else if (a[mid] < value) {      low = mid + 1;    } else {      high = mid - 1;    }  }  return -1;}

python实现：

def binary_search(arr: list, value) -> int:
    low, high = 0, len(arr) - 1    while low <= high:
        mid = low + ((high - low) >> 1)
        if arr[mid] == value:
            return mid
        elif arr[mid] > value:
            high = mid - 1        else:
            low = mid + 1    return -1  # 未找到返回-1

low、high、mid 都是指数组下标，其中 low 和 high 表示当前查找的区间范围，初始 low=0， high=n-1。mid 表示 [low, high] 的中间位置。我们通过对比 a[mid] 与 value 的大小，来更新接下来要查找的区间范围，直到找到或者区间缩小为 0，就退出。

需要注意的点：

1.循环退出条件是 low<=high，而不是 low<high。

2.mid=(low+high)/2 这种写法，在 low 和 high 比较大时，两者之和可能会溢出。

改进的方法是将 mid 的计算方式写成 low+(high-low)/2，转化成位运算 low+((high-low)>>1)更佳。

3.写成 low=mid 或者 high=mid，可能会发生死循环。应当写成low=mid+1，high=mid-1。