二叉查找树是最常用的一种二叉树,它支持快速插入、删除、查找操作,各个操作的时间复杂度跟树的高度成正比,理想情况下,时间复杂度是 O(logn)。但二叉查找树在频繁的动态更新过程中,可能会出现树的高度远大于 log2n 的情况,从而导致各个操作的效率下降。极端情况下,二叉树会退化为链表,时间复杂度会退化到 O(n)。要解决这个复杂度退化的问题,需要设计一种平衡二叉查找树。
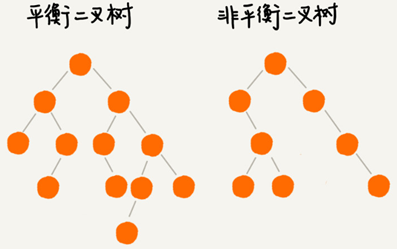
平衡二叉树的严格定义是任意一个节点的左右子树的高度相差不能大于 1。
完全二叉树、满二叉树都是平衡二叉树,非完全二叉树也有可能是平衡二叉树。

1570444901543
最先被发明的平衡二叉查找树是AVL 树,它严格符合平衡二叉查找树的定义,即任何节点的左右子树高度相差不超过 1,是一种高度平衡的二叉查找树。
但是很多平衡二叉查找树并没有严格符合上面的定义(树中任意一个节点的左右子树的高度相差不能大于 1),比如红黑树,它从根节点到各个叶子节点的最长路径,有可能会比最短路径大一倍。
发明平衡二叉查找树这类数据结构的初衷是,解决普通二叉查找树在频繁的插入、删除等动态更新的情况下,出现时间复杂度退化的问题。
所以,平衡二叉查找树中“平衡”的意思,其实就是让整棵树左右看起来比较“对称”、比较“平衡”,不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些,相应的插入、删除、查找等操作的效率高一些。
所以,只要树的高度不比 log2n 大很多(树的高度仍然是对数量级的),就仍然可以认为这是一个合格的平衡二叉查找树。
绝大部分情况下Treap、Splay Tree操作的效率都很高,但是也无法避免极端情况下时间复杂度的退化。尽管这种情况出现的概率不大,但是对于单次操作时间非常敏感的场景来说,它们并不适用。
AVL 树是一种高度平衡的二叉树,所以查找的效率非常高,但AVL 树为了维持这种高度的平衡,每次插入、删除都要做调整比较复杂、耗时。对于有频繁的插入、删除操作的数据集合,使用 AVL 树的代价就有点高。
红黑树只是做到了近似平衡,并不是严格的平衡,所以在维护平衡的成本上,要比 AVL 树要低。红黑树的插入、删除、查找各种操作性能都比较稳定。对于工程应用来说,要面对各种异常情况,为了支撑这种工业级的应用更倾向于这种性能稳定的平衡二叉查找树。
动态数据结构支持动态地数据插入、删除、查找操作
散列表:插入删除查找都是O(1), 是最常用的,但其缺点是不能顺序遍历以及扩容缩容的性能损耗。适用于那些不需要顺序遍历,数据更新不那么频繁的。
跳表:插入删除查找都是O(logn), 并且能顺序遍历。缺点是空间复杂度O(n)。适用于不那么在意内存空间的,其顺序遍历和区间查找非常方便。